How the Charles Law Formula Revolutionizes Understanding of Ideal Gas Behavior

At the intersection of temperature, pressure, and volume, the Charles Law Formula stands as a cornerstone of thermodynamics, revealing how ideal gases behave under changing conditions. When temperature is held constant, volume changes inversely with pressure—a relationship defined by V ∝ 1/T, yet fundamentally encoded in the broader Charles Law framework that underpins gas laws. This principle not only explains everyday phenomena but also drives innovations in engineering, climate science, and industrial processes.

Understanding how Charles Law quantifies this inverse proportionality transforms abstract concepts into practical tools essential for scientists and engineers alike.

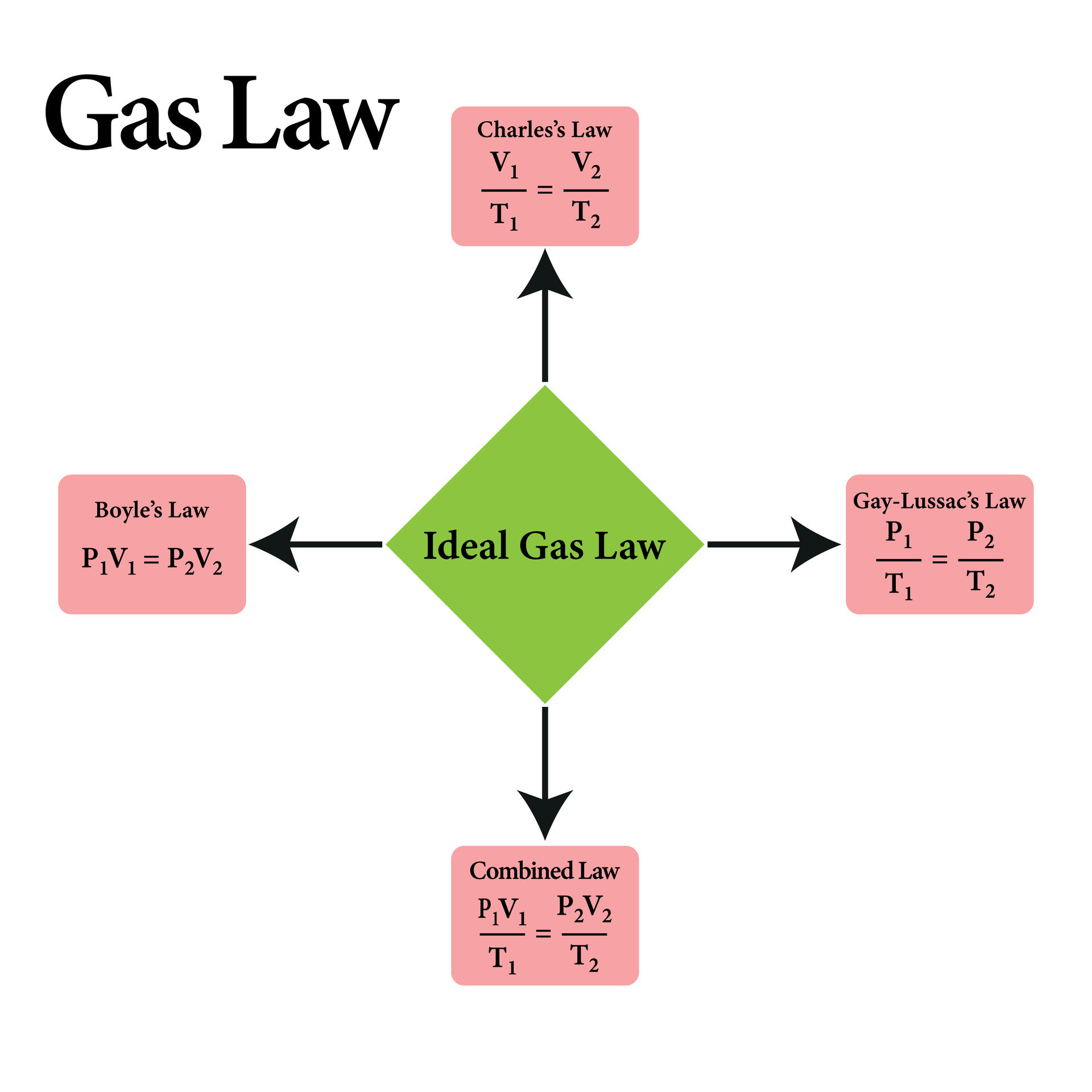
Discovered in the 18th century by Jacques Charles and later formalized, the law establishes that for a fixed mass of gas at constant temperature, the volume it occupies is directly proportional to its absolute temperature measured on the Kelvin scale. This relationship—often remembered through the simplified formula V₁/T₁ = V₂/T₂—offers precise predictions about gas expansion and contraction. “The Charles Law formula is not just theoretical; it’s a predictive engine,” notes Dr.

Elena Marquez, a thermodynamics expert at MIT. “It allows engineers to design systems where gas behavior must be precisely controlled.”

Core Principles: The Mathematics and Meaning of V ∝ 1/T

The Charles Law formula is most commonly expressed as V = k·T, where V represents volume, T the absolute temperature in Kelvin, and k a proportionality constant unique to each gas. This linear relationship reveals a foundational truth: gases expand as temperature rises and contract when cooled—assuming pressure remains unchanged.

The shift from Celsius to Kelvin is critical here; absolute zero (0 K) marks the theoretical limit where gas particles cease motion, and volumes collapse to zero according to the law:

• At 273 K (0°C), a gas occupies a defined baseline volume—often taken as 22.4 liters per mole of an ideal diatomic gas like nitrogen or oxygen.
• Doubling the temperature to 546 K elevates volume to 44.8 liters under isothermal conditions.
• Conversely, cooling halves the volume, illustrating gas compression: cooling natural gas pipelines prevents pressure surges and structural damage.

“This inverse connection between volume and temperature isn’t just a curiosity—it’s the physics behind pressure regulation,” explains chemical engineer Raj Patel, “Understanding Charles Law explains why hot air balloons rise (warmer air expands), why inner-tire pressure spikes in summer heat, and how industrial reactors maintain safe operating ranges.”

Historical Context and Scientific Foundations

The Charles Law formula belongs to a broader framework encapsulated by the ideal gas law, which combines multiple gas behavior principles into a single equation. Yet, Charles Law retains unique utility in analytical scenarios involving constant pressure or volume, where its simplicity enables rapid calculations.

“Even with the advent of computational thermodynamics, solving for temperature straightforwardly using V ∝ 1/T remains essential in outreach and education,” says Dr. Marquez.

Real-World Applications: From Climate Science to Industrial Engineering

The versatility of Charles Law manifests across scientific and industrial domains.

In climate science, the law helps model atmospheric behavior: as air rises and cools, its expansion and reduced density influence cloud formation and wind patterns. Similarly, weather balloons measure temperature changes by tracking volume shifts in gas-filled instruments suspended from the ground.

Industrial applications are equally profound. Pressure vessels in chemical plants rely on Charles Law to predict volume changes under varying heat loads—critical for preventing explosive decompression.

HVAC systems use calibrated expansions of refrigerants governed by this principle to maintain consistent cooling efficiency. Even medical applications emerge: understanding how breathing gases expand and contract with temperature fluctuations aids respiratory device design.

“The Charles Law formula underpins safety calculations in aerospace too,” says aerospace engineer Linda Cho. “In rocket combustion chambers, extreme heating causes gas expansion; knowing these dynamics prevents catastrophic pressure failures.”

Limitations and Ideal Assumptions

Despite its power, Charles Law applies strictly only under ideal conditions—constant pressure and in gases with negligible molecular volume and intermolecular forces.

Real gases deviate near extreme temperatures or pressures, requiring corrections via equations like van der Waals. “It’s vital to recognize that Charles Law is a first-order approximation,” warns Dr. Marquez.

“Engineers must factor in real gas behavior when precision matters—beyond basic educational models.”

The Enduring Impact of Charles Law Formula

The Charles Law Formula transcends classroom lessons to become a vital analytical tool grounded in elegant simplicity. By linking volume, temperature, and absolute scale in a predictable, proportional relationship, it equips scientists and engineers with actionable insights into gas behavior. Whether predicting weather patterns, optimizing industrial reactors, or launching weather balloons into the stratosphere, this 18th-century discovery remains a touchstone of modern thermodynamics.

As technology advances, its role persists—clearing the path from theoretical physics to real-world innovation. Understanding how gases respond to heat through Charles Law is not just a testament to scientific progress but a practical key to mastering the invisible forces shaping daily life and industrial success.