The Degrees to Radians Formula You Can’t Afford to Ignore in Math and Science

For engineers, physicists, mathematicians, and students navigating angles, rotational motion, or circular trigonometry, the transition from degrees to radians is not just routine—it’s essential. Unlike degrees, which are based on a tomb-infrought 360-part division of a circle, radians define angles through the geometry of the circle itself, making them indispensable in calculus, complex analysis, and physics. The Degrees to Radians Formula—radians = degrees × (π/180)—unlocks this deeper mathematical language, transforming raw angular measures into values compatible with trigonometric functions and Fourier transforms.

Understanding its utility and application reveals why mastering this simple conversion is a cornerstone of technical literacy across STEM fields.

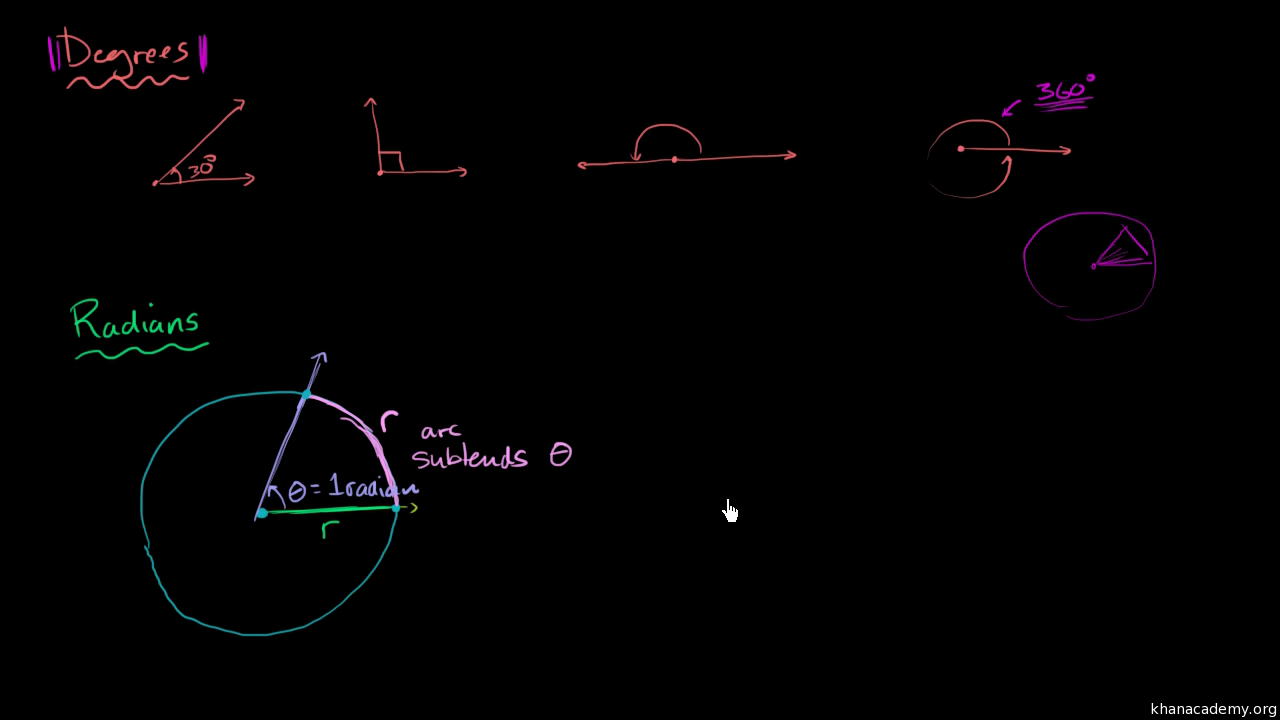
The Degrees to Radians Formula Explained: At its core, the conversion hinges on a single, elegant mathematical relationship: radians = degrees × (π / 180). This ratio arises from the fact that a full circle spans 360 degrees, while the circumference corresponds to 2π radians.

Since arc length (s) equals radius (r) times angle in radians (s = rθ), setting s = 2r (for a full circle) gives θ = 2π radians—confirming that 360° = 2π rad. Solving for radians per degree yields the foundational formula: radians = degrees × π/180. This precise conversion preserves angular relationships without approximation, a critical advantage when working with limits, integrals, or differential equations involving angle measures.

To illustrate, consider how this formula transforms real-world scenarios.

Suppose a rotating motor turns 150 degrees—what angular displacement is this in radians? Applying the formula: radians = 150 × (π / 180) = (5π / 6) ≈ 2.618 rad. Now imagine a planet orbiting its star with an angular velocity of 0.25 rad per day—radians simplify modeling acceleration and orbital dynamics.

In electrical engineering, radians standardize phase angles in AC circuits, ensuring consistency across calculations. Because trigonometric functions in most mathematical software—like Python’s `math` module or MATLAB—expect input in radians, this conversion acts as a vital interface between human intuition (degrees) and machine precision (radians).

Why Radians Matter More Than Degrees in Advanced Mathematics

Beyond conversion mechanics, radians are preferred because they reflect the intrinsic link between arc length and angle. In calculus, the derivative of sin x is simply cos x only when x is measured in radians.

For example, lim(h→0) [sin(h)/h] = 1 is mathematically true only at radian values; misapplying degrees distorts this limit, breaking foundational calculus principles. Similarly, integrals involving periodic functions, Fourier series expansions, and differential equations involving angular frequency all require radians for accuracy and coherence. As renowned mathematician and author David Burton notes in Mathematics: A Very Short Introduction, “Radians are not arbitrary—they embed the geometry of motion, making them the natural unit for angular quantities in science.”

Consider rotational kinematics: an object spinning at 60 degrees per second has angular velocity of (60 × π/180) = π/3 radians per second.

A stroke of intuition—linking linear speed to angular rate—relies on radians to ensure equations like v = rω scale correctly, without factor-of-π confusion. This precision ripples through robotics, astronomy, planetary science, and even computer graphics, where smooth rotation algorithms depend on radian-based precision to animate scenes without jitter or distortion.

Real-World Examples: From Engineering to Everyday Tech

In mechanical engineering, radians govern gear ratios, crankshaft motion, and rotational sensors. A CNC machine interpreting angular commands must convert user input from degrees to radians to control spindle speed accurately.

Likewise, GPS satellites accumulate angular changes in radians to compute trajectories, where even minor degree-to-radian miscalculations could misplace a vehicle by meters.

In signal processing, radians simplify Fourier transforms, which decompose complex waves into sinusoidal components. When analyzing alternating currents or audio frequencies, using radians ensures the mathematical model captures true phase shifts and harmonic relationships.

Mobile device gyroscopes and accelerometers output angular rates in degrees, but underlying algorithms process these in radians—ensuring that a 360°/s rotation translates correctly to 2π rad/s, preserving timing and sensitivity.

Step-by-Step: Mastering the Degrees-to-Radians Formula

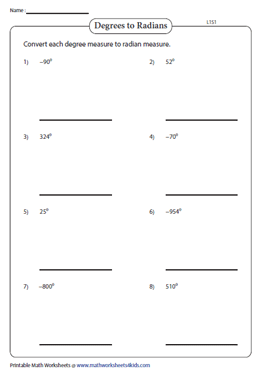
To consistently apply the formula with speed and accuracy: 1. Identify the angle in degrees (e.g., consider 45°). 2.

Multiply by π (approximately 3.14159). 3. Divide the product by 180—this scales the degree value to radians using the ratio 180/π.

For example: 45° × (π / 180) = (45/180) × π = (1/4)π = π/4 radians. This process works for all angles—from 0° up to 360°, or even beyond into full circles and multiple rotations. When dealing with negative angles (e.g., −90°), the same formula applies, yielding −π/2 rad, signaling clockwise rotation from the positive axis.

Visualization aids reflection: imagine unwinding a circle. Each full 360° loops back to 2π rad, illustrating why 180° equals π rad—half a circle. This spatial intuition reinforces that radians capture angle as arc length divided by radius, a geometric truth embedded in the formula itself.

The Global Standard: Radians in Academic and Industrial Frameworks

Scientific journals, university curricula, and international standards bodies—including the International Bureau of Weights and Measures—adopt radians as the universal unit for angular measurement.

This standardization prevents ambiguity in technical documentation, research papers, and global engineering projects. Translating degrees to radians is not merely computational—it’s a step toward universal linguistic alignment in science. As physics professor Marcus Du Sautoy observes, “Radians are not a niche detail—they are the syntax of modern physics, enabling precise, concise expression of rotational phenomena.”

Textbooks from MIT OpenCourseWare to IB Math courses emphasize radians early, treating them as fundamental alongside pi and i, reinforcing their role in calculus, linear algebra, and beyond.

In seem Eich tests and standardized exams, conversions test comprehension—ensuring students grasp the interplay between units and underlying geometry, not memorized formulas. This