The Logarithm of 3: A Gateway to Understanding Exponentials, Scale, and Complexity
The Logarithm of 3: A Gateway to Understanding Exponentials, Scale, and Complexity
What defines magnitude in vastly different systems—from earthquake intensity to information theory? The logarithm of 3 emerges as a subtle yet powerful mathematical lens, revealing patterns in nature, technology, and abstract science. Though seemingly simple, log₃(3) holds profound implications: it confirms that 3 is the unique unit where exponential growth aligns precisely with base-3 scaling, making it indispensable in fields ranging from signal processing to fractal geometry.
This number transcends arithmetic, acting as a bridge between discrete magnitude and continuous measurement, with applications that shape modern computation and physical modeling.
Decoding the Math: What Log₃(3) Truly Represents
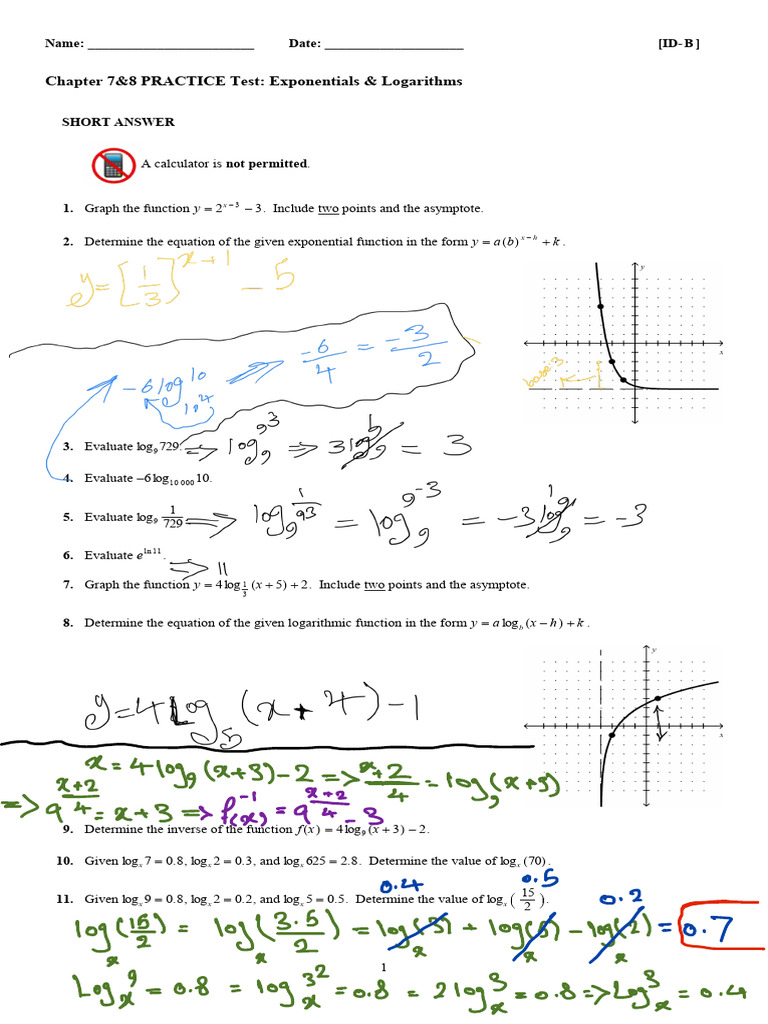
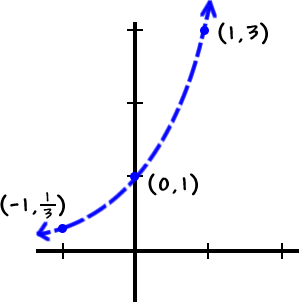
Logarithms answer a fundamental mathematical question: to what power must a base be raised to produce a given number? Formally, log₃(3) = x means: ³ˣ = 3. Since 3 raised to the first power equals 3, the solution is x = 1.
This elegance makes log₃(3) exact and clean—no approximation, no ambiguity. | Base | log₃(3) | Value of x | |------|---------|------------| | 3 | log₃(3) | 1 |
Unlike other logarithmic expressions involving variables or complex numbers, log₃(3) resists misinterpretation. It is unambiguous: the logarithm of a number to its own base collapses to unity, a cornerstone in exponential algebra.
This precision supports accurate modeling in domains where error margins matter—such as satellite signal calibration or digital communication systems, where base-3 encoding enhances clarity.
Logarithm of 3 in Nature and Physical Systems
In natural phenomena, logarithmic scales quantify processes where change accelerates or decelerates exponentially. Though base 10 or base *e* dominate these scales, base-3 logarithms appear where ternary logic or trinomial structures govern behavior. For example, in crystal lattice analysis, the number of stable atomic configurations within a unit cell often aligns with powers of three, making log₃ essential for modeling symmetry and packing efficiency.
In seismology, the moment magnitude scale compares earthquake energies, but behind the scenes, logarithmic transformations normalize data across orders of magnitude. While not typically base-3, the principle extends: understanding magnitude in steps often hinges on logarithms whose bases reflect system physics. When natural patterns align with ternary division—such as in quarks (three fundamental charges) or Platonic solids (three-dimensional simplicity)—log₃ becomes a natural analytical tool.
Moreover, fractal systems—self-similar structures repeating across scales—frequently exhibit logarithmic depth logarithms tied to base 3. Each branching level may triple complexity, captured mathematically through repeated application of log₃, revealing hidden order in apparent chaos.
Engineering, Computing, and the Role of Log₃(3)
In digital communication, base-3 encoding enhances error detection and penetration in noisy channels.
Ternary signaling—transmitting data via three distinct states—optimizes spectral efficiency, analogous to base-10 in conventional radio. Logarithm of 3 underpins such systems: calculating data throughput, bandwidth allocation, and signal-to-noise ratios often reveals coefficients involving log₃(3), ensuring engineers size components and allocate resources accurately. Computing architectures depth its roots in ternary logic in niche applications.
Early theoretical computers explored ternary computation using three-state logic (high, medium, low voltage), where each state transition mathematically involves log₃ relationships. Though dominant systems use binary codification, research into numeric computing—such as balanced ternary—for reduced power consumption and improved parallelism keeps log₃ relevant. In signal processing, Fourier and wavelet transforms decompose signals across frequency, often requiring logarithmic representations to compress dynamic ranges.
Base-3 transforms simplify certain fractal or self-similar signals, where applications of log₃ help quantify dimensionality and scaling behaviors, bridging numerical analysis and physical interpretation.
The Enduring Relevance of Logarithm of 3
Beyond niche areas, log₃(3) anchors broader mathematical coherence. As a dimensionless constant of scale, it validates the consistency of exponential relationships across disciplines—physics, informatics, and material science alike.
Its exactness provides a baseline for approximation; when modeling systems growing multiplicatively by threes, log₃(3) ensures fidelity. Consider epidemic modeling: if infection spreads through tripling transmission rates per generation, log₃(3) confirms that each cycle advances the outbreak by a factor of 3. Similarly, in quantum mechanics, base-3 symmetries in group theory classify particle states, with log₃(3) revealing the branching complexity inherent to physical laws.
Everywhere logarithms stabilize exponential dynamics, log₃(3) stands as a precise sentinel—simple, yet profound. Its value of 1 is more than arithmetic convenience: it reflects the unity between base and exponent, exposing depth in systems where magnitude evolves multiplicatively. Whether quantifying natural symmetry, optimizing digital signals, or simplifying complex transformations, log₃(3) endures as a fundamental unit of scale and logic, indispensable to both theory and practice.
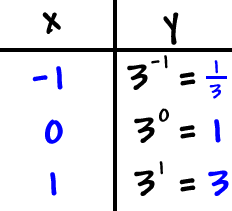
Related Post
Diane Sawyer ABC Bio Wiki Age Family Husband Children Salary and Net Worth

Julia Roberts 2024: The Enduring Star Who Redefines Timelessness

A Closer Look at the Woman Behind the Anchor: The Life and Legacy of David Muir’s Wife
Stranger Things Star Noah Schnapp Relationship Status: Decoding the Latest Buzz and Public Appearances

