Unlocking Derivative Precision: Mastering Inverse Function Derivatives Through Formulas and Real-World Examples
Unlocking Derivative Precision: Mastering Inverse Function Derivatives Through Formulas and Real-World Examples
From refining machine learning models to optimizing complex engineering systems, the ability to compute inverses and their derivatives lies at the heart of advanced calculus. Inverse function derivative formulas provide a powerful mathematical lens to analyze how outputs respond to inputs when a function’s inverse is differentiable. These tools bridge abstract theory and practical computation, empowering scientists and engineers to model dynamic systems with exceptional accuracy.
This article explores the core formula behind inverse derivatives, breaks down its derivation with clarity, and showcases its application through concrete examples—revealing how abstraction fuels real-world precision.
The Core Formula: How to Derive the Derivative of an Inverse Function
At the heart of inverse function derivatives lies a deceptively simple yet profoundly useful formula: If a differentiable function \( y = f(x) \) has an inverse function \( x = f^{-1}(y) \), then the derivative of the inverse at a point is given by \[ \frac{d}{dy} [f^{-1}(y)] = \frac{1}{\frac{d}{dx} [f(x)]} \quad \text{at } y = f(x). \] In other words, the slope of the inverse function at \( y \) equals the reciprocal of the slope of the original function at the corresponding \( x \)-value.This elegant relationship stems from the inverse function theorem, a cornerstone of calculus that ensures the existence of a smooth inverse under regularity conditions. When \( f(x) \) is continuously differentiable and its derivative is non-zero near \( x \), then \( f^{-1}(y) \) is also differentiable, and the inverse derivative formula provides a direct computational shortcut. To derive this, consider the definition of inverse functions: \( x = f^{-1}(y) \) implies \( y = f(x) \).
Differentiating both sides with respect to \( y \) yields: \[ 1 = \frac{dy}{dx} \cdot \frac{dx}{dy}, \] which rearranges to \[ \frac{dx}{dy} = \frac{1}{\frac{dy}{dx}}. \] This derivation confirms that the derivative of the inverse function depends fundamentally on the reciprocal of the original function’s derivative.
Why This Formula Matters: The Mathematical Foundation
Understanding the inverse derivative formula is more than an academic exercise—it is a gateway to solving nonlinear inverse problems efficiently.In calculus, computing derivatives exactly for transformed functions is often intractable using basic rules, but applying this formula allows precise, closed-form expressions when \( f(x) \) is invertible. For instance, dealing with logarithmic, exponential, or transcendental functions frequently requires inverting variables to proceed with differentiation or optimization. The formula also underpins more advanced calculus concepts, including implicit differentiation, parametric curve analysis, and the calculation of partial derivatives in multivariable settings.
By mastering inverse derivatives, practitioners gain a portable toolkit for transformations central to physics, economics, and machine learning.
Worked Example: Derivative of an Inverse Function in Action
To amplify understanding, consider the function \( f(x) = e^x \), a cornerstone of calculus and exponential modeling. Its inverse is \( f^{-1}(y) = \ln(y) \), the natural logarithm.Step 1: Compute the derivative of \( f(x) \): \[ f'(x) = \frac{d}{dx} e^x = e^x. \] Step 2: Apply the inverse derivative formula at \( y = e^x \): \[ \frac{d}{dy} [\ln y] = \frac{1}{e^x}. \] But since \( y = e^x \), we substitute back: \[ \frac{d}{dy} [\ln y] = \frac{1}{y}.
\] This confirms the well-known result: the slope of \( \ln y \) at \( y = e^x \) is exactly \( 1/e^x \), consistent with logarithmic behavior. Another test case: let \( f(x) = x^3 + 2x + 1 \), a nonlinear but differentiable function. Its inverse \( f^{-1}(y) \) satisfies \( f(f^{-1}(y)) = y \).
While no elementary inverse exists, the formula applies formally: at \( y = f(x) \), \[ \frac{d}{dy} [f^{-1}(y)] = \frac{1}{f'(x)} = \frac{1}{3x^2 + 2}. \] Although \( x = f^{-1}(y) \) cannot be expressed simply here, the derivative formula remains valid for any point on
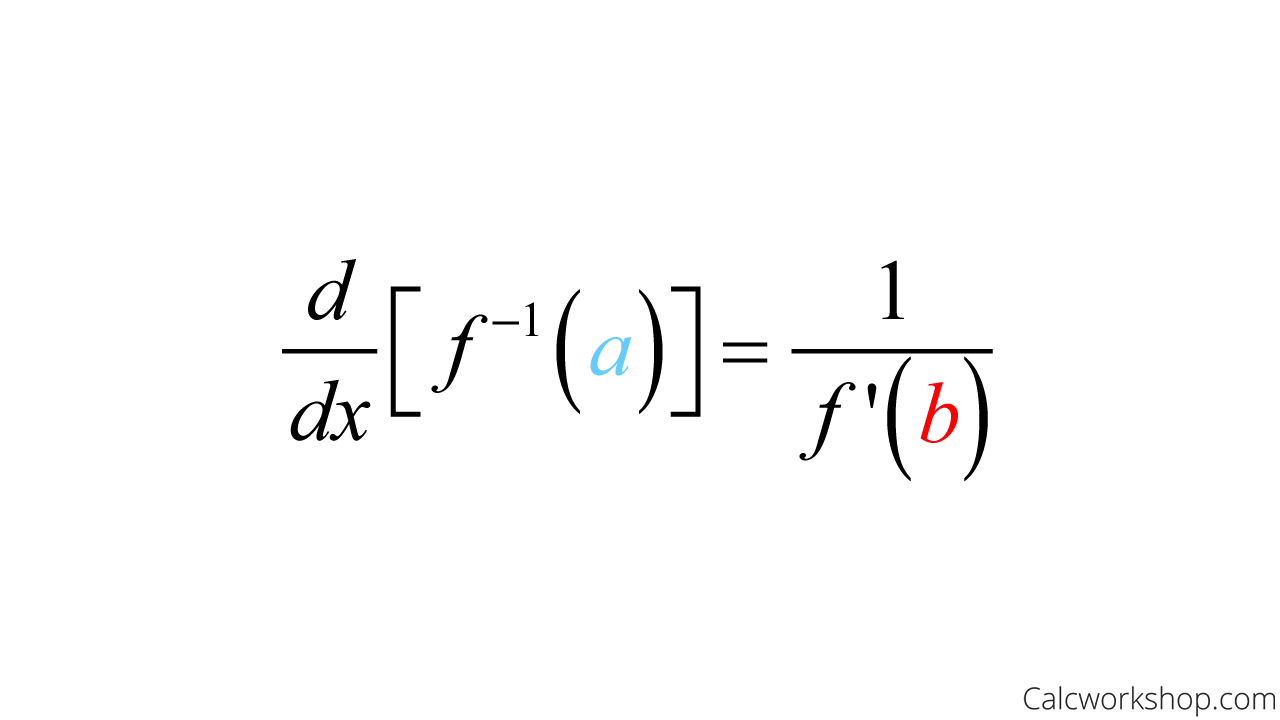
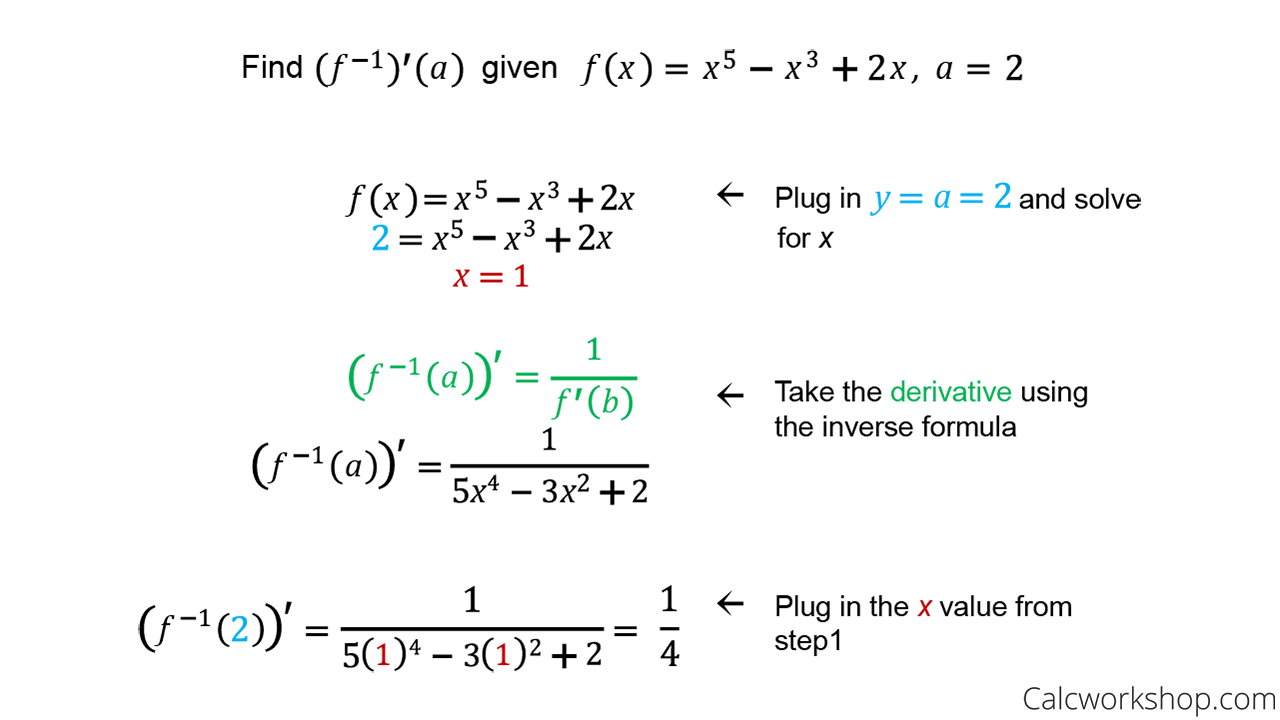

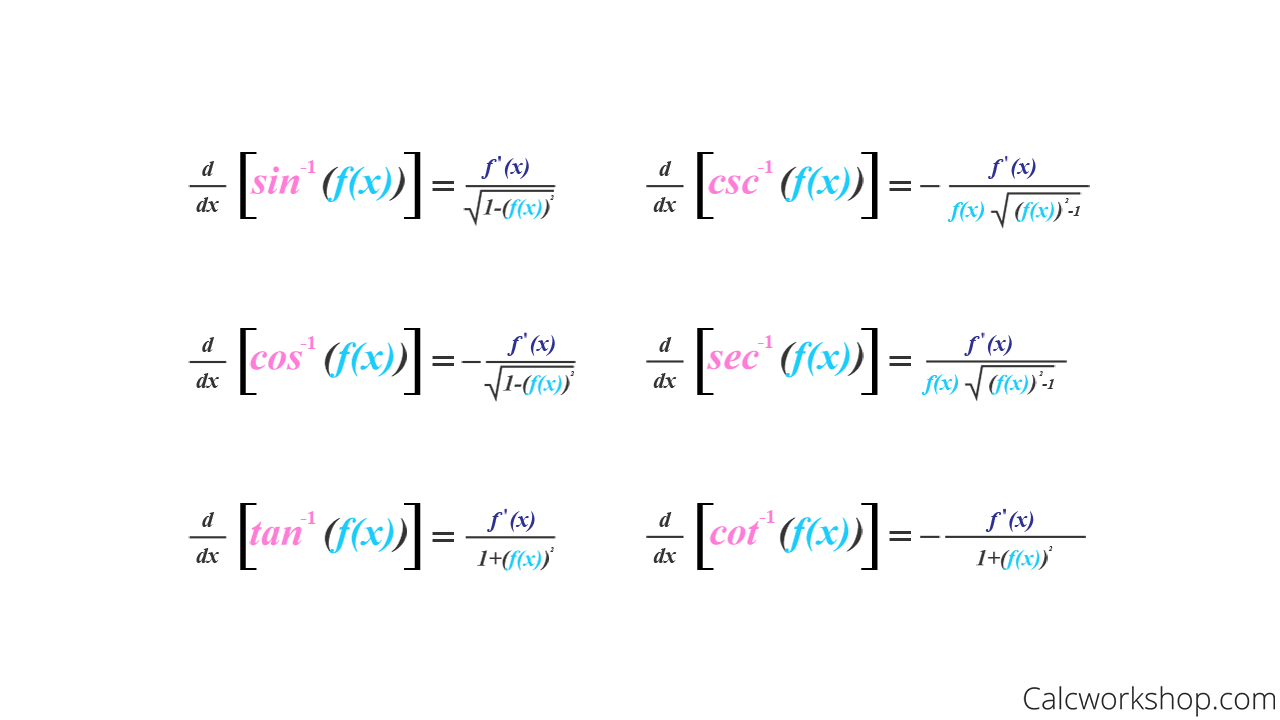
Related Post

Adventure Time: Where Cartoons Dive Deep into the Human Soul Through Arrived-Kai Characters

Unlock Short Being: How DigitalPuzzles Turn Mental Gymnastics into Daily Adventure
Danielle Nicolet Family Matters Bio Wiki Age Husband Movies and Net Worth

Vince Offer’s Gilded Success: The Untold Wealth, Height, Age, and Legacy of a Pitchmans Dynasty

