Unlocking the Secrets of the Mandelbrot Fractal: A Journey into Mathematical Wonder

Beneath the surface of chaotic beauty lies one of mathematics’ most captivating creations—the Mandelbrot fractal—whose infinite complexity unfolds with every magnified zoom. Known for its hypnotic symmetry and boundless detail, this fractal is not merely a visual phenomenon but a profound illustration of self-similarity and nonlinear dynamics. Far more than a digital curiosity, the Mandelbrot set reveals deep truths about order emerging from complexity, inviting scientists, artists, and dreamers alike into a realm where infinity meets imagination.

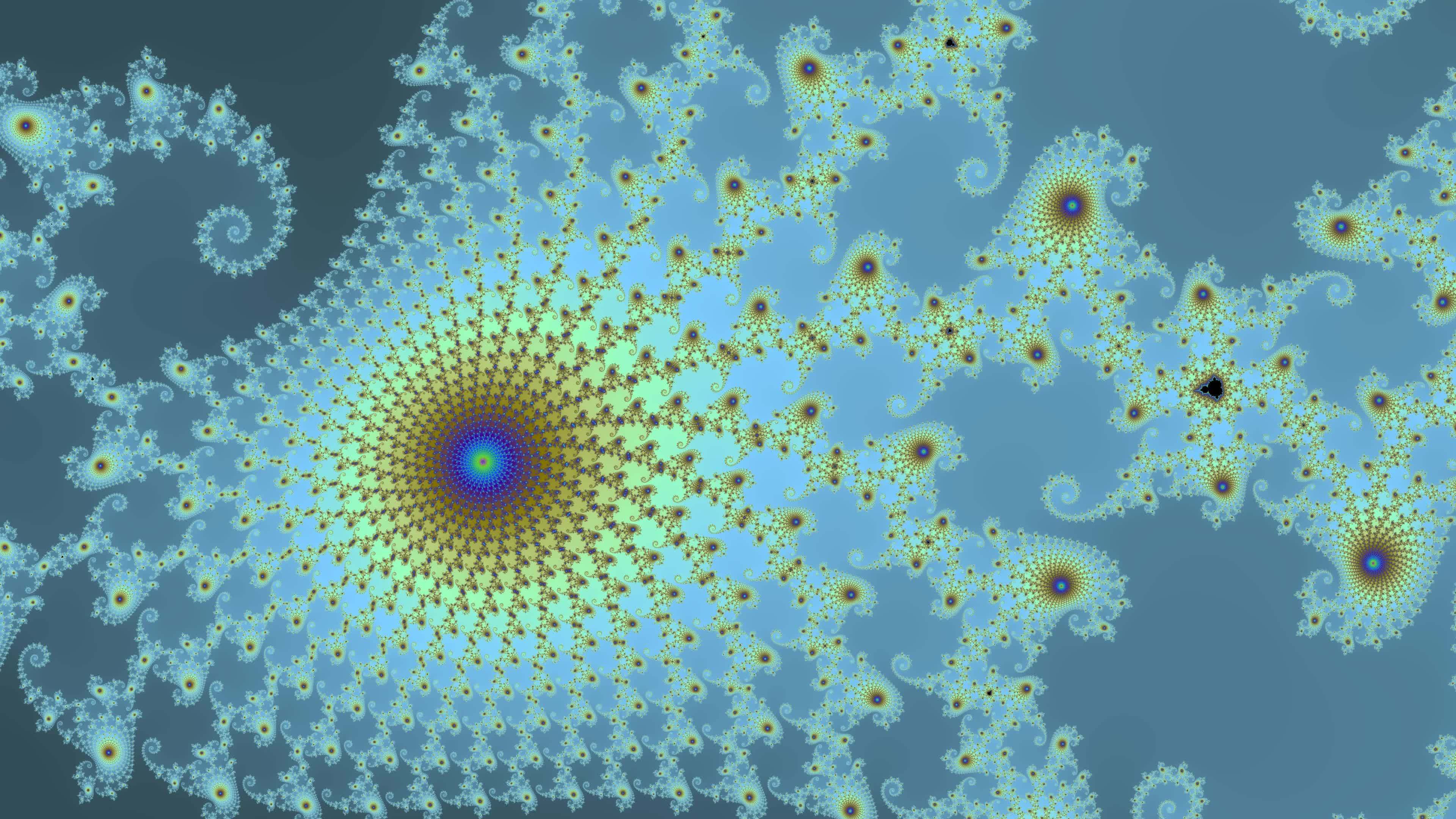
At the heart of this phenomenon lies a deceptively simple iterative formula: zₙ₊₁ = zₙ² + c. Here, z is a complex number, and c is a constant in the complex plane—each value of c determines whether the sequence remains bounded or spirals into chaos. When plotted across a grid of complex numbers, this rule generates the Mandelbrot fractal, a boundary between stability and divergence shimmering with intricate shapes.

“What begins as a void becomes a masterpiece,” notes mathematician Heinz-Otto Peitgen, capturing the essence of how the fractal transforms simplicity into obsession. The visual spectacle arises from the fractal’s self-similar structure: zooming into any edge reveals recurring patterns at ever-smaller scales, a hallmark of fractal geometry. These miniature replicas, though never identical, share the same mathematical DNA, echoing the infinite regress inherent in recursive systems.

Each loop in the boundary exposes new structures—Cardioids, Seahorses, Disks—each governed by precise computational logic yet evolving into astonishing visual diversity.

Mathematicians trace the Mandelbrot set’s origins to the late 1970s, though its full depth remained hidden until advances in computing brought it into sharp focus. English theologian and mathematician Benoit Mandelbrot, after whom the set is named, sought to describe irregular forms in nature—coastlines, clouds, mountain ridges—that resist classical geometry.

“We live in a fractal world,” he once asserted, a prescient insight linking mathematical abstraction to natural phenomena. The Mandelbrot fractal embodies this idea, revealing how fundamental recurrence shapes both abstract space and the tangible universe. The technical foundation rests on iteration and escape time algorithms.

For each point c in the plane, researchers compute how quickly the sequence zₙ escapes to infinity. Points inside the set stay bounded, forming a solid, dark region—typically black or deep blue—while those outside diverge rapidly, rendering them vibrant hues in visualizations. This color coding does more than aestheticize data; it encodes quantitative information, mapping the speed of divergence with precise precision.

The computational demands of rendering the Mandelbrot fractal have driven innovation in algorithmic efficiency and graphics rendering. Early explorations relied on basic recursive code, but modern implementations leverage GPU acceleration and level-of-detail rendering techniques to explore billions of iterations at ultra-high resolution. These advancements allow scientists to study convergence properties, fractal dimensions, and even connections to deeper mathematical theories such as dynamical systems and chaos theory.

The fractal’s boundary, a Tipler-like limiter, remains endlessly complex—no matter how closely observed, new features always emerge, defying finite description. Beyond its scientific implications, the Mandelbrot fractal has permeated culture and art. Its mesmerizing patterns inspire digital artists, musicians, and designers, who translate its recursive beauty into immersive installations and algorithmic compositions.

The fractal serves as a metaphor for discovery—each zoom a metaphor for curiosity, each detail a reminder of hidden order beneath apparent chaos. As researcher Hans Magnus Enzensberger reflects, “The Mandelbrot set is not just a shape; it is a legend that connects human thought to the infinite.”

Mathematically, the set’s boundary is a nowhere-differentiable, ultra-complex curve with Hausdorff dimension exactly 2—bridging topology, measure theory, and computational geometry. Its study bridges pure theory and applied science: fractal dimensions inform modeling in physics, image compression, and signal processing—fields where traditional linear models fall short.

In this way, the Mandelbrot fractal acts as both a profound abstract concept and a practical tool for innovation. What makes the Mandelbrot fractal truly mesmerizing is not just its visual flair, but its embodiment of emergence—the way complexity arises from simple rules. “It’s a laboratory for studying how order arises from initial simplicity,” explains physicist and complexity theorist Christopher Langton.

From cryptographic applications to cosmological simulations, the principles underlying this fractal extend far beyond geometry into realms of computation, biology, and even consciousness studies. In essence, the Mandelbrot fractal transcends categorization: part mathematical construct, part cosmic fingerprint, part artistic wonder. Its persistence across scales mirrors nature’s own patterns—from explosions to snowflakes—where minute mechanisms give rise to vast, intricate wholes.

As technology evolves, so too does our capacity to explore its depths, uncovering new layers with each computational advance. The fractal is finite in creation but infinite in discovery—an enduring invitation to question, observe, and marvel.

In pursuing the Mandelbrot fractal, we do more than appreciate beauty; we engage with the fundamental processes shaping reality.

Its recursive elegance challenges conventional boundaries between art and science, complexity and simplicity, chaos and order. In every zoom, new layers reveal themselves—not just of numbers and sets, but of the human spirit’s unceasing quest to understand the invisible patterns that govern the universe. That is the true power of the Mandelbrot fractal: it distills infinity into a singular, unfolding image, forever inviting exploration into the mesmerizing unknown.